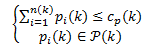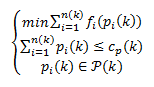The number of electric vehicles is increasing at a worldwide level. For instance, 12 000 electric cars were sold in the US country in January 2017, accounting for approximately 1% of the total US auto sales. This results into a Year over Year (YoY) increase of about 59% [1]. Similarly, the Chinese market had more than 32 000 new electric cars along the streets in March 2017, which corresponds to an 89% increase over the same month last year, with the YoY increase now at 31% [2]. Numbers in Europe are contradictory, as the penetration level strongly depends on the specific country. For instance, new registrations for battery powered cars increased in the first quarter of 2017 from 23703 to 32607 in the EU, Norway and Switzerland [3]. In particular, countries in Northern Europe are leading the way (e.g., UK, Netherlands, Scandinavian countries). For instance, Norway has the highest per capita number of all-electric cars in the world: more than 100 000 in a country of 5.2 million people [4].
The main reason behind such numbers is undoubtedly the growing concerns over environmental issues. To address them, governments have exerted a regulatory pressure to reduce urban pollution, in most cases through appropriate incentives to purchase electric vehicles, and to facilitate the creation of a charging infrastructure. The pressure is also expected to further increase the upcoming years, as some countries are taking even more strict measures. For instance, Paris, Madrid, Athens and Mexico City are planning to ban the most polluting cars and vans by 2025 to tackle air pollution, while they promote electric vehicles and cleaner transport [5]. Such restrictive measures are expected to further increase the penetration level of electric vehicles, and some projections (e.g., Bloomberg [6]) predict that electric vehicles might account for 35% of all new vehicle sales (worldwide) in 2040. Obviously, this implies that much larger penetration levels may be reached in specific areas.
The previous numbers and predictions are obviously creating some concerns regarding the ability of the power grid to accommodate such a new electric load. On the other hand, electric vehicles may be also regarded as an opportunity, as at the same time they might not just take electricity from the grid (G2V, as the power flows from the Grid to the Vehicles), but also occasionally inject power in the grid (V2G). In this sense, a fleet of electric vehicles plugged into the grid may be also regarded as a possible virtual battery connected to the grid.
Accordingly, the next sections investigate the mathematical problems arising in this context. In doing so, we shall mainly follow the recent reference [7]. Also, we shall intend the notion of Electric Vehicles (EVs) in the broadest sense, i.e., by EVs we shall both refer to Fully Electric Vehicles (FEVs) and to Plug-in Hybrid EVs (PHEVs).
Charging of Electric Vehicles
The charging problem can be modelled as (1):
where is the power drawn by the i’th vehicle at time step k. If we assume that n(k) are plugged to the power grid at the same time, then the power drawn by the population of the fleet of vehicles cannot exceed a maximum value (i.e., ) that depends on the total power available for charging. Such maximum threshold depends itself on many variables, as on the amount of other loads connected to the same bus, the topology and the constraints of the power grid, possibly the power locally generated from renewable sources. At the same time, the second equation of (1) shows that the power drawn by the i’th vehicle cannot take arbitrary values, but is set to lie on a predetermined set of feasible charging powers. At this regard, it is possible to distinguish three main categories:
- On-off charging, where the value of can either be 0 (no charging) or equal to the maximum value (e.g., 4kW in the case of standard single phase outlets). Examples in this direction can be found in [8-9].
- Multi-level charging, where the value of can be chosen among of a set of possible values. For instance, the vehicle may be charged in a fast mode at off-peak times, while it may be charged in a slow mode at on-peak times. Other intermediate charging speeds may be possible as well to further accomplish a larger variety of charging solutions.
- Continuously adaptable charging, when the value of can continuously adjust its power rate, within the feasible set (i.e., between 0 – no charging - and a maximum value given by the power rate of the outlet).
Note that the optimisation problem (1) can be interpreted as a resource allocation problem, where the shared resource (i.e., maximum power) must be shared among a set of vehicles. Note that in principle many different ways may be devised to share the power among the vehicles. While an obvious solution may be to give the same power to all vehicles, problem (1) becomes most interesting when one optimally shares the available power in order to further minimise a cost function of interest, i.e. (2),
In the optimisation problem (2), we further have that the cost functions indicate some cost associated with receiving a given instantaneous power . In most cases; this may refer to the price for charging, to the overall time required for charging; or the inconvenience for the users associated with a given power; or the inconvenience for the grid (i.e., in terms of its overall availability to serve the requested total demand for charging); or may measure some CO2 emissions associated with a given charging (e.g., depending on whether power generated from renewable sources is available or not for charging EVs). Obviously, problem (2) may be also formulated as a maximisation problem, in the case one assumes that the functions represent some utility of interest (e.g., revenues).
A number of algorithms have been proposed in the literature to solve problem (2). Different solutions may be categorised as:
- Distributed vs. centralised solutions: In the case of centralised solutions, each EV communicates to some central infrastructure its charging needs (i.e., how much they should charge, and by what time). The central infrastructure gathers all this information and computes the optimal scheduling in order to minimise a cost function of interest. Examples in this direction can be found in [10-12]. While centralised solutions may more efficiently solve the optimisation problem (as the central infrastructure has all the information required to solve the optimisation problem), they are known not to be as robust, and communication efficient as distributed solutions. For this reason, it is usually advocated that a mixed framework, where some central infrastructure is interfaced with some local controllers may be the most convenient trade-off [13]. Other examples of distributed solutions are [14-18].
- Cooperative vs. competitive solutions: In the resource-allocation formulation of the electric vehicle charging problem, EVs may either cooperate or compete to get a larger share of the shared resource (i.e., to complete their charging as soon as possible). While competing scenarios may occur when EV owners pursue opportunistic strategies, cooperative solutions may arise when the EV owners are all employees of the same company, or EV car-sharing service. Examples of both solutions may be found in the already mentioned [15], while examples of competing solutions are [19-21]. Note that in most of these papers where competing behaviours are considered, game-theory based methodologies are employed to solve them.
Problem extensions
The optimisation problem (2) can be further refined and made more realistic along a number of different lines. In particular, the following problems are of interest in the related literature:
- V2G, as briefly anticipated, EVs may provide a number of ancillary services to the grid, especially considering that vehicles are idle (i.e., parked) most of the time. Under the assumption that vehicles may be plugged to the grid every time they are parked, then the grid would have a giant virtual battery at its own disposal, that can be used to improve the functioning of the grid (e.g., in terms of active and reactive power exchange, for peak-shaving/valley filling purposes, and more in general to accomplish demand side management tasks, to mitigate problems associated with voltage drops, power losses or overheating). Some works that have addressed V2G issues are [22-23, 16].
- V2B and B2V, more recently, some part of the literature concerned about V2G ancillary services has specialised upon the particular case of power exchanged between electric vehicles and buildings - Vehicle to Building (V2B) and Building to Vehicle (B2V). In fact, batteries of EVs may be used as an alternative to conventional in-home batteries to implement demand side management functionalities in buildings. In particular, power generated from photovoltaic (PV) panels (e.g., on the roof of a building) can be used to charge EVs if at the same time domestic appliances are switched off. Similarly, power can be occasionally taken from EVs to drive domestic appliances when power from renewable sources is not available. Examples of papers along this line of research are [24-27].
- Topology of the grid, many of the aforementioned works tend to neglect the actual topology of the grid. In this case, the main assumption is that all EVs are connected to the same sub-station or to the same bus. While such an assumption may hold in the case of a single microgrid, still it might be unsatisfactory when a realistic large-scale scenario is actually considered. Among the works that explicitly take the topology of the grid into account we remind [28-29].
- Privacy preserving aspects become important when EV owners are not willing to reveal their needs (i.e., how much energy should be required and by what time) to some central infrastructure or to some kind of an aggregator. Whenever this kind of information is considered to be sensitive, then algorithms that do not reveal this kind of information become important. Additive Increase Multiplicative Decrease (AIMD) algorithms are known to be very convenient both in terms of reduced communication requirements, and also in terms of their privacy preserving properties. More information at this regard can be found in [7, Chapter 18].
- Receding horizon solutions come into play anytime one is not interested in instantaneously solving problem (2) (i.e., in a greedy fashion), but rather in finding the optimal solution in a future horizon of time. Then the problem becomes much more complicated as it requires the ability to compute the optimal solution considering the highly uncertain scenario. The uncertainties entering the optimisation problem regard the need to predict the future driving/charging patterns of EV owners; and also the future power generation (e.g., from renewable sources) and future load consumption. Note that all such uncertain future profiles are themselves related to other aspects (i.e., meteorological conditions affect power generation, load consumption, and also energy consumption in EVs). Papers addressing this issue are [30], where Particle Swarm Optimization (PSO) method is used, [31], where a Markov decision process is used, and [32], where a robustified version of a heuristic algorithm based on Model Predictive Control (MPC) is employed.
References
[1] https://cleantechnica.com/2017/02/04/us-electric-car-sales-59-january-2017/, last accessed: May 2017.
[2] https://evobsession.com/china-electric-car-sales-keep-soaring-march-2017/, last accessed: May 2017.
[3] https://www.bloomberg.com/news/articles/2017-05-04/electric-car-sales-are-suddenly-taking-off-in-europe, last accessed: May 2017.
[4] http://e360.yale.edu/features/with-norway-in-the-lead-europe-set-for-breakout-on-electric-vehicles, last accessed: May 2017.
[5] https://www.theguardian.com/environment/2016/dec/02/four-of-worlds-biggest-cities-to-ban-diesel-cars-from-their-centres, last accessed: May 2017.
[6] https://www.bloomberg.com/features/2016-ev-oil-crisis/, last accessed: May 2017.
[7] E. Crisostomi, R. Shorten, F. Wirth and S. Stüdli, “Electric and Plug-in Hybrid Vehicle Networks: Optimization and Control”, CRC Press – Taylor & Francis, Series: Automation and Control Engineering, 2017.
[8] S. Stüdli, R.H. Middleton, and J.H. Braslavsky, “A fixed-structure automaton for load management of electric vehicles”. In Proc. IEEE European Control Conference (ECC), pages 3566-3571, Zurich, Switzerland,
July 2013.
[9] L. Yao, W. H. Lim, and T. S. Tsai, “A Real-Time Charging Scheme for Demand Response in Electric Vehicle Parking Station”, IEEE Transactions on Smart Grid, vol. 8, no. 1, pp. 52-62, 2017.
[10] S. Deilami, A.S. Masoum, P.S. Moses, and M.A.S. Masoum, “Real-time coordination of plug-in electric vehicle charging in smart grids to minimize power losses and improve voltage profile”, IEEE Transactions on
Smart Grid, vol. 2, no. 3, pp. 456-467, 2011.
[11] K. Clement-Nyns, E. Haesen, and J. Driesen, “The impact of charging plug-in hybrid electric vehicles on a residential distribution grid”, IEEE Transactions on Power Systems, vol. 25, no. 1, pp. 371-380, 2010.
[12] W. Su and M.-Y. Chow, “Performance evaluation of an EDA-based largescale plug-in hybrid electric vehicle charging algorithm”, IEEE Transactions on Smart Grid, vol. 3, no. 1, pp. 308-315, 2012.
[13] J.A. Peças Lopes, F.J. Soares, and P.M. Rocha Almeida, “Integration of electric vehicles in the electric power system”, Proceedings of the IEEE, vol. 99, no. 1, pp. 168-183, 2011.
[14] D. Wu, D.C. Aliprantis, and L. Ying, “Load scheduling and dispatch for aggregators of plug-in electric vehicles”, IEEE Transactions on Smart Grid, vol. 3, no. 1, pp. 368-376, March 2012.
[15] S. Stüdli, E. Crisostomi, R. Middleton, and R. Shorten, “A flexible distributed framework for realising electric and plug-in hybrid vehicle charging policies”, International Journal of Control, vol. 85, no. 8, pp. 1130-1145, 2012.
[16] E.L. Karfopoulos, K.A. Panourgias, and N.D. Hatziargyriou, “Distributed coordination of electric vehicles providing V2G regulation services”, IEEE Transactions on Power Systems, vol. 31, no. 4, pp. 2834-2846, 2016.
[17] L. Gan, U. Topcu, and S.H. Low, “Optimal decentralized protocol for electric vehicle charging”, IEEE Transactions on power systems, vol. 28, no. 2, pp. 940-951, 2013.
[18] S. Grammatico, “Exponentially convergent decentralized charging control for large populations of plug-in electric vehicles”, in Proc. IEEE Conference on Decision and Control (CDC), pp. 5775-5780, Las Vegas, Nevada, December 2016.
[19] M. Gonzales Vaya, S. Grammatico, G. Andersson, and J. Lygeros, “On the price of being selfish in large populations of plug-in electric vehicles”, 54th IEEE Conference on Decision and Control (CDC), pp. 6542-6547, Osaka, Japan, December 2015.
[20] S. Grammatico, F. Parise, M. Colombino, and J. Lygeros, “Decentralized convergence to Nash equilibria in constrained deterministic mean field control,” IEEE Transactions on Automatic Control, vol. 61, no. 11, pp. 3315-3329, 2016.
[21] S. Zou, Z. Ma, X. Liu, and I. Hiskens, “An Efficient Game for Coordinating Electric Vehicle Charging”, IEEE Transactions on Automatic Control, vol. 62, no. 5, pp. 2374-2389, 2017.
[22] S. Stüdli, E. Crisostomi, R. Middleton, and R. Shorten. “Optimal real-time distributed V2G and G2V management of electric vehicles”, International Journal of Control, vol. 87, no. 6, pp. 1153-1162, 2014.
[23] Y. Ota, H. Taniguchi, J. Baba, and A. Yokoyama, “Implementation of autonomous distributed V2G to electric vehicle and DC charging system”, Electric Power Systems Research, vol. 120, pp. 177-183, March 2015.
[24] E. Ancillotti, R. Bruno, E. Crisostomi and M. Tucci, “Using Electric Vehicles to Improve Building Energy Sustainability”, in Proc. of IEEE International Electric Vehicle Conference (IEVC), Florence, Italy, 2014.
[25] D. Wu, H. Zeng, C. Lu, and B. Boule, “Two-Stage Energy Management for Office Buildings With Workplace EV Charging and Renewable Energy”, IEEE Transactions on Transportation Electrification, vol. 3, no. 1, pp. 225-237, 2017.
[26] C. Pang, P. Dutta, and M. Kezunovic, “BEVs/PHEVs as Dispersed Energy Storage for V2B Uses in the Smart Grid”, IEEE Transactions on Smart Grid, vol. 3, no. 1, pp. 473-482, 2012.
[27] H.K. Nguyen, and J.B. Song, “Optimal Charging and Discharging for Multiple PHEVs with Demand Side Management in Vehicle-to-Building”, IEEE Journal of Communications and Networks, vol. 14, no. 6, pp. 662-671, 2012.
[28] J. de Hoog, T. Alpcan, M. Brazil, D.A. Thomas, and I. Mareels, “Optimal charging of electric vehicles taking distribution network constraints into account”, IEEE Transactions on Power Systems, vol. 30, no. 1, pp. 365-375, 2015.
[29] G. Deconinck, K. De Craemer, and B. Claessens, “Combining Market-Based Control with Distribution Grid Constraints when Coordinating Electric Vehicle Charging”, Engineering, vol. 1, no. 4, pp. 453-465, 2015.
[30] A. Y. Saber and G. K. Venayagamoorthy, “Resource scheduling under uncertainty in a smart grid with renewables and plug-in vehicles”, IEEE Systems Journal, vol. 6, no. 1, pp. 103-109, March 2012.
[31] E. B. Iversen, J.M. Morales, and H. Madsen, “Optimal charging of an electric vehicle using a Markov decision process”, Applied Energy, vol. 123, pp. 1-12, 2014.
[32] S. Zao, X. Lin, and M. Chen, “Robust Online Algorithms for Peak-Minimizing EV Charging under Multi-Stage Uncertainty”, IEEE Transactions on Automatic Control, accepted for publication, 2017.
Contributor:
Dr Emanuele Crisostomi, University of Pisa